3. Grid and Coordinates¶

Related CPP options:

CURVGRID	Activate curvilinear coordinate transformation
SPHERICAL	Activate longitude/latitude grid positioning
MASKING	Activate land masking
WET_DRY	Activate wetting-Drying scheme
NEW_S_COORD	Choose new vertical S-coordinates

Preselected options:

# define CURVGRID
# define SPHERICAL
# define MASKING
# undef WET_DRY
# undef NEW_S_COORD

3.1. Vertical Grid parameters¶

Two vertical transformations are available for the generalized vertical terrain-following vertical system : By default, we have :

\begin{eqnarray} z(x,y,\sigma,t) & = & z_0(x,y,\sigma) + \zeta(x,y,t) \left[ 1+\frac{z_0(x,y,\sigma)}{h(x,y)} \right] \\ z_0 (x,y,\sigma) & = & h_c \sigma + \left[ h(x,y) -h_c \right] Cs(\sigma) \end{eqnarray}

When activating the cpp key NEW_S_COORD, we have:

\begin{eqnarray} z(x,y,\sigma,t) & = & \zeta(x,y,\sigma) + \left[ \zeta(x,y,t) + h(x,y) \right] z_0(x,y,\sigma) \\ z_0 (x,y,\sigma) & = & \frac{ h_c \sigma + h(x,y)Cs(\sigma)}{h_c+h(x,y)} \end{eqnarray}

with :

\(z_0 (x,y,\sigma)\) a nonlinear vertical transformation
\(\zeta (x,y,\sigma)\) the free-surface
\(h(x,y)\) the ocean bottom
\(\sigma\) a fractional vertical stretching coordinate, \(-1 \le \sigma \le 0\)
\(h_c\) a positive thickness controlling the stretching
\(Cs(\sigma)\) a nondimensional, monotonic, vertical stretching, \(-1 \le (C\sigma) \le 0\)

Vertical grid stretching is controlled by the following parameters, which have to be set similarly in croco.in, and crocotools_param.m:

theta_s	Vertical S-coordinate surface stretching parameter. When building the climatology and initial CROCO files, we have to define the vertical grid. Warning! The different vertical grid parameters should be identical in this crocotools_param.m and in croco.in. This is a serious cause of bug.
theta_b	Vertical S-coordinate bottom stretching parameter.
hc	Vertical S-coordinate Hc parameter. It gives approximately the transition depth between the horizontal surfacelevels and the bottom terrain following levels. (Note it should be inferior to hmin in case of Vtransform =1).

Then we have, with \(N\) the number of vertical levels:

with the old transformation :

\[Cs(\sigma)=(1-\theta_b) \frac{sinh(\theta_s \ \sigma)}{sinh(\theta_s)} + \theta_b \left[ \frac{0.5 \ tanh\left( \left(\sigma+0.5 \right)\theta_s \right) }{ tanh (0.5 \ \theta_s) } - 0.5 \right]\]

with NEW_S_COORD defined :

\begin{eqnarray} sc & = & \frac{\sigma-N}{N} \\ csf & = & \frac{1.-cosh(\theta_s \ sc)}{cosh(\theta_s)-1.} \quad \textrm{if} \ \theta_b > 0 , \quad csf=-sc^2 \quad \textrm{otherwise}\\ Cs(\sigma) & = & \frac{e^{\theta_b csf}-1.}{1.-e^{-\theta_b}} \quad \qquad \textrm{if} \ \theta_s > 0 , \quad Cs(\sigma)=csf \quad \textrm{otherwise} \end{eqnarray}

Other parameters have to be set to prepare the grid file in crocotools_param.m:

vtransform	S-coordinate type (1: old- ; 2: new- coordinates). It is associated to #NEW_S_COORD cpp-keys in CROCO source code.
hmin	Minimum depth in meters. The model depth is cut at this level to prevent, for example, the occurrence of model grid cells without water. This does not influence the masking routines. At lower resolution, hmin should be quite large (for example, 150m for dl=1/2). Otherwise, since topography smoothing is based on, the bottom slopes can be totally eroded.
hmax_coast	Maximum depth under the mask. It prevents selected isobaths (here 500 m) from going under the mask. If this is the case, this could be a source of problems for western boundary currents (for example).
hmax	Maximum depth
rtarget	This variable controls the maximum value of the -parameter that measures the slope of the sigma layers (Beckmann and Haidvogel, 1993): To prevent horizontal pressure gradient errors, well in terrain-following coordinate models (Haney, 1991), realistic topography requires some smoothing. Empirical results have shown that reliable model results are obtained if it does not exceed 0.2.
n_filter_deep_topo	Number of passes of a Hanning filter to prevent the occurrence of noise and isolated seamounts on deep regions.
n_filter_final	Number of passes of a Hanning filter at the end of the smoothing process to be sure that no noise is present in the topography.

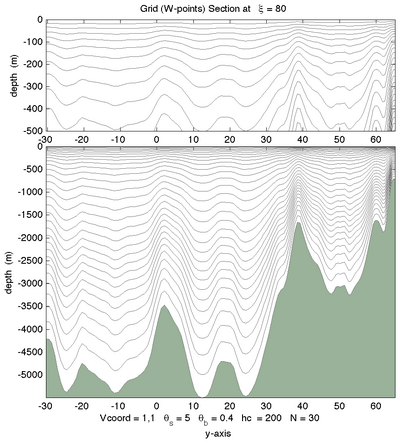
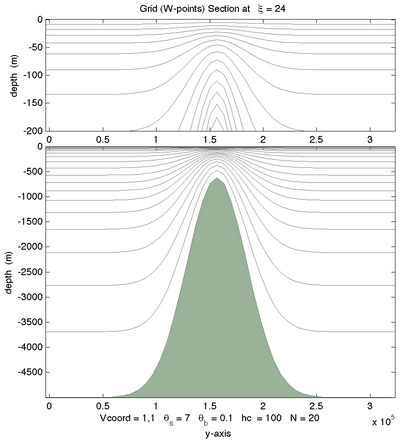
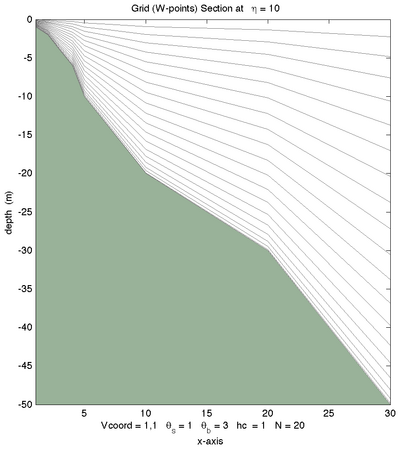
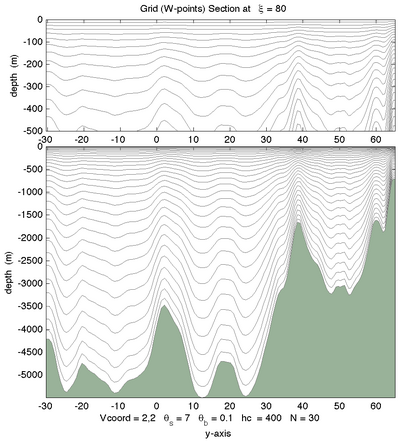
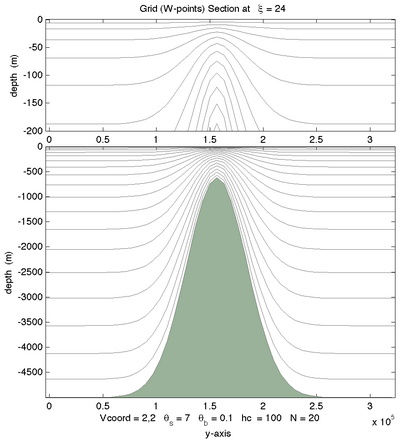
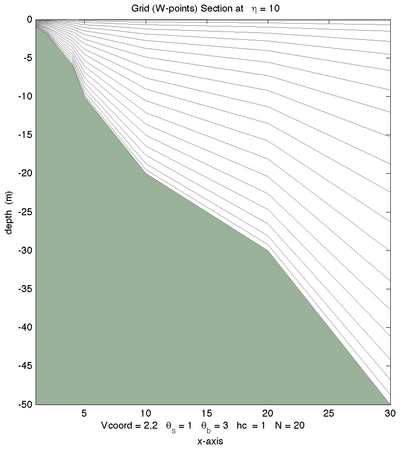
The effects of theta_s, theta_b, hc, and N can be tested using the Matlab script : croco_tools/Preprocessing_tools/test_vgrid.m

Below are some examples of different vertical choices (Courtesy of ROMS-RUTGERS team) :


Vtransform=1, \(\theta_S=7.0, \theta_B=0.1\)	Vtransform=1, \(\theta_S=7.0, \theta_B=1.0\)	Vtransform=1, \(\theta_S=7.0, \theta_B=3.0\)

Vtransform =1, \(\theta_S=7.0,\theta_B=1.0\)	Vtransform=2, \(\theta_S=7.0, \theta_B=1.0\)	Vtransform=2, \(\theta_S=7.0, \theta_B=3.0\)

3.2. Grid staggering¶

The discretization is based on a staggered grid where not all variables are stored at the same grid points.

The free-surface (zeta), density (rho), and active/passive tracers (t) are located at the center of the cell whereas the horizontal velocity (u and v) are located at the edges of the cell.

   ----  v(i,j+1)  ----
  |                    |
  |                    |
u(i,j)   rho(i,j)   u(i+1,j)
  |                    |
  |                    |
   ----   v(i,j)   ----

More information about this and the array indices when using MPI parallelisation is given in staggered grids.

3.3. Wetting-Drying¶

The Wetting-Drying scheme is derived from John Warner’s code (Rutgers ROMS) and adapted to the time stepping scheme of CROCO. The main idea is to cancel the outgoing momentum flux (not the incoming) from a grid cell if its total depth is below a threshold value (critical depth Dcrit between 5 and 20 cm according to local slope; Dcrit min and max adjustable in param.h). This scheme is tested in the Thacker case producing oscillations in a rotating bowl for which an analytical solution is known.